“It’s not the destination, it’s the journey.” – Ralph Waldo Emerson
Over the last six months many investors have been reminded of what volatility can look like across many assets and asset classes alike. Increased volatility may or may not be over, but as educated investors, we all know that there is no individual out there that can predict future markets consistently. With that knowledge, this month (and in future newsletters) we’re going to take a deep dive into understanding how to measure risk and recognize that all returns are not created equal. As Ralph Waldo Emerson brilliantly said, “It’s not the destination, it’s the journey”.
Many investors are satisfied knowing their portfolio is allocated between stocks, bonds, and cash and the expected return is 6.5% (in later examples, we’ll call this portfolio, the ‘Fat Tail Portfolio’). That seems reasonable on the surface, but what if I told you historically that portfolio has experienced losses greater than 30% six times in its history. You might not think so favorably about that 6.5% return now that you have been provided some information on risk!
On the other hand, we have another portfolio (we’ll call this the ‘Even Distribution Portfolio’), which has an identical 6.5% annualized return, but never had a one-year loss greater than 6%. I imagine many of you would be selling your Fat Tail Portfolio and reallocating to this Consistent Returns Portfolio.
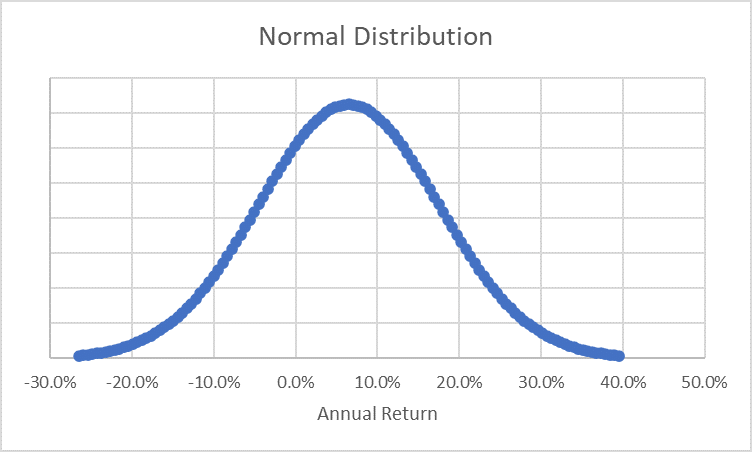
This exact scenario should tell us that as investors we must not only consider returns, but also spend time understanding risk. There are many ways to measure risk and the general investment world has taken to measuring risk using standard deviation. Standard deviation is a measure of how spread out numbers are. The more spread out the numbers, the higher the standard deviation. If we have a portfolio with a wide variation of returns it is going to have a high standard deviation. First, standard deviation is based off the notion that over long periods of time an investment will have a normal distribution of returns (see below) meaning most annual returns will be clustered around the average return and fewer and fewer returns will exist as we move further away from the average.
Unfortunately, we don’t live in a normal world and rarely do investments portray the returns of a normal distribution.
Our hypothetical portfolios above (Fat Tails Portfolio & Even Distribution Portfolio) have the following characteristics:
Fat Tails Portfolio
Annualized Return = 6.5%
Standard Deviation = 10.9%
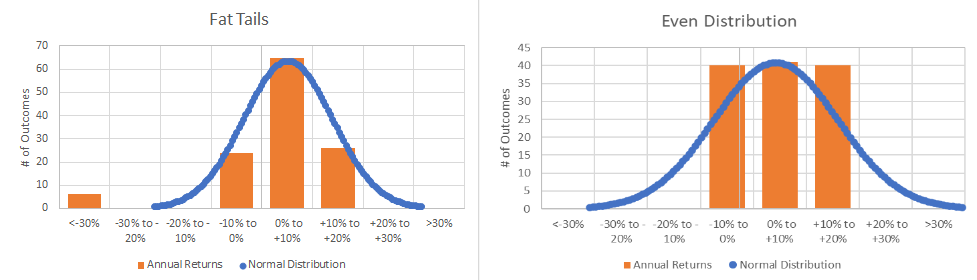
Annual Returns of the “Fat Tails” Portfolio Compared to a Normal Distribution
Even Distribution Portfolio
Annualized Return = 6.5%
Standard Deviation = 10.2%
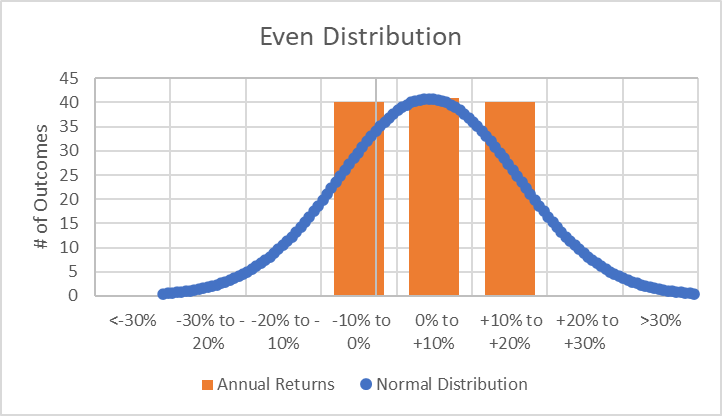
Annual Returns of the “Even Distribution” Portfolio Compared to a Normal Distribution
Viewing these returns compared to a normal distribution presents a new issue for us. Standard deviation is measured based on the assumption that over time returns will look like a normal distribution, but clearly these two examples, which are based on 121 years of returns, are nowhere near a normal distribution!
WARNING: Entering the Nerd Zone
Now that we understand the flaw in standard deviation for investment portfolios, we must find more accurate measures of the shape of the returns to help us clarify which portfolio is best for our investment futures.
These two measures are called skew and kurtosis.
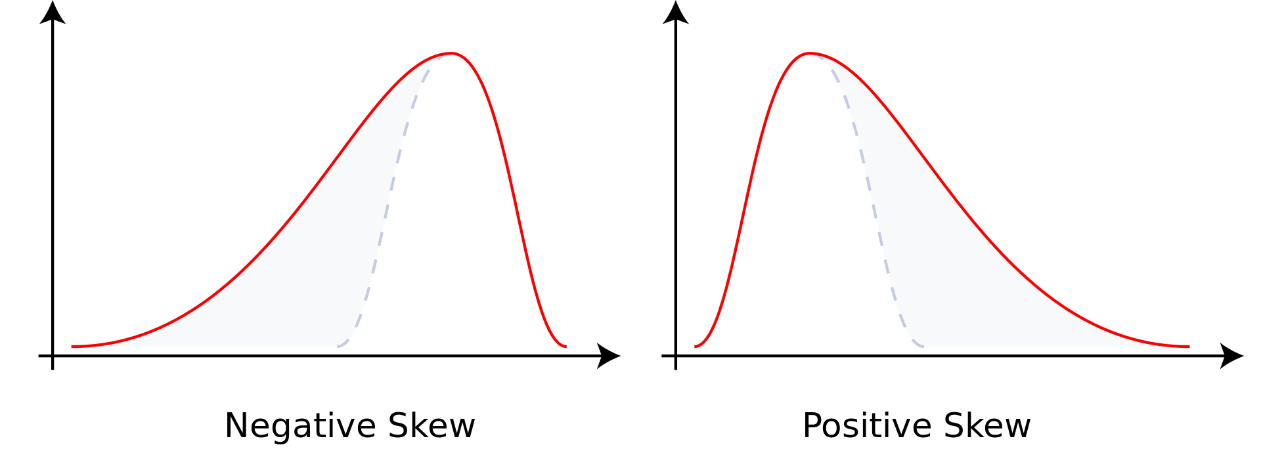
Skewness is the measure of asymmetry in the distributions of returns. Since the normal distribution we discussed above has perfect symmetry, the skew is 0. As the number of larger negative returns (otherwise known as a ‘tail’) increase, the distribution becomes asymmetric with a negative tail. As a result, the skew would be represented by a negative number. Inversely, consistent returns with a few outsized positive returns (figure on the right below) will provide a positive skew.
Kurtosis on the other hand only measures the size of the tails, positive or negative. A positive kurtosis means that there are many outliers either positive or negative. If all returns are bunched evenly between -1% & +15%, then there would be no tails. As a result, that chart would have a negative kurtosis.
Let’s take a look at some examples to help explain.
From our two sample portfolios above (Fat Tails & Even Distribution) here is the skew and kurtosis for each:
Skew -2.0 Skew -0.2
Kurtosis 5.3 Kurtosis -1.5
This tells us that a negative skew is concerning in that we might experience large negative returns at some point in the future. Kurtosis on the other hand, should be thought of as complimentary to skew, rather than valuable on its own. A large kurtosis with a positive skew could signify a tremendous opportunity while a large kurtosis with a negative skew (Fat Tails Portfolio) tells us to be cautious of potential large negative returns.
Now let me ask you, we have four portfolio options with the following Annualized Returns & Standard Deviations. Which one would you want?
| Name | Fat Tails | Consistent Returns | Even Distributions | Big Hits |
| Annualized Return | 6.5% | 6.5% | 6.5% | 5.8% |
| Standard Dev | 10.9% | 7.3% | 10.2% | 18.0% |
Hopefully, your response would be “I need more information”. Because once you see the Skew & Kurtosis (plus the graph) the choice becomes much clearer.
| Name | Fat Tails | Consistent Returns | Even Distributions | Big Hits |
| Annualized Return | 6.5% | 6.5% | 6.5% | 5.8% |
| Standard Dev | 10.9% | 7.3% | 10.2% | 18.0% |
| Skew | -2.0 | 0.9 | -0.2 | 4.8 |
| Kurtosis | 5.3 | -0.7 | -1.5 | 22.6 |
Now that you have all the information, I believe many investors would strongly consider the “Big Hits” portfolio which has the lowest annualized return and the highest standard deviation! The “Big Hits” portfolio may only average a 5.8% return, but we know from its positive skew that any deviation from that average return will typically be on the positive side of 5.8%. Additionally, with such a high kurtosis, many of those positive returns will be located way up in the positive tail of its distribution. Translation: with a portfolio like this, we won’t experience large downswings like in the other portfolios. As Ralph Waldo Emerson brilliantly stated years ago, “It’s not the destination, it’s the journey.” Maybe Mr. Emerson was well ahead of his time and trying to explain portfolio analysis when he exclaimed that memorable quote!
In an upcoming newsletter we will consider a few final statistical measures now that we all understand that Standard Deviation may not provide you a proper understanding when comparing portfolio options.
As always, your team at iNNOVA Wealth Partners is here to help you with all your financial planning, investment guidance, and overall wealth management needs.
iNNOVA Wealth Partners, LLC (“iNNOVA”) is a registered investment advisor. Information presented herein is for educational purposes only and does not intend to make an offer or solicitation for the sale or purchase of any specific securities, investments, or investment strategies. Investments involve risk and unless otherwise stated, are not guaranteed.
Readers of the information contained on these performance reports, should be aware that any action taken by the viewer/reader based on this information is taken at their own risk. This information does not address individual situations and should not be construed or viewed as any typed of individual or group recommendation. Be sure to first consult with a qualified financial adviser, tax professional, and/or legal counsel before implementing any securities, investments, or investment strategies discussed.
The case studies/examples and results included are for illustration purposes only and may not be typical.
Any tax information and estate planning information contained herein is general in nature, is provided for informational purposes only, and should not be construed as legal or tax advice. iNNOVA does not provide legal or tax advice. iNNOVA cannot guarantee that such information is accurate, complete, or timely. Laws of a particular state or laws that may be applicable to a particular situation may have an impact on the applicability, accuracy, or completeness of such information. Federal and state laws and regulations are complex and are subject to change. Changes in such laws and regulations may have a material impact on pre- and/or after-tax investment results. iNNOVA makes no warranties with regard to such information or results obtained by its use. iNNOVA disclaims any liability arising out of your use of, or any tax position taken in reliance on, such information. Always consult an attorney or tax professional regarding your specific legal or tax situation.
iNNOVA has been nominated for and has won several awards. iNNOVA did not make any solicitation payments to any of the award sponsors in order to be nominated or to qualify for nomination of the award.